REPRESENTASI PENGETAHUAN : LOGIKA PROPOSISI

Logika dan Set

• Representasi pengetahuan dengan symbol logika merupakan bagian dari penalaran eksak.
• Bagian yang paling penting dalam penalaran adalah mengambil kesimpulan dari premis.
• Logika dikembangkan oleh filusuf Yunani, Aristoteles (abad ke 4 SM) didasarkan pada silogisme, dengan dua premisdan satu konklusi.
• Contoh :

1. Premis : Semua laki-laki adalah makhluk hidup
2. Premis : Socrates adalah laki-laki
3. Konklusi : Socrates adalah makhluk hidup

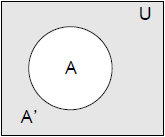
• Cara lain merepresentasikan pengetahuan adalah dengan Diagram Venn. 

• Diagram Venn merepresentasikan sebuah himpunan yang merupakan kumpulan objek.
• Objek dalam himpunan disebut elemen.

1. A ={1,3,5,7}
2. B = {….,-4,-2,0,2,4,…..}
3. C = {pesawat, balon}

• Symbol epsilon εmenunjukkan bahwa suatu elemen merupakan anggota dari suatu himpunan, contoh : 1 εA . Jika suatu elemen bukan anggota dari suatu himpunan maka symbol yang digunakan ∉, contoh : 2 ∉A.
• Jika suatu himpunan sembarang, misal X dan Y didefinisikan bahwa setiap elemen X merupakan elemen Y, maka X adalah subset dari Y, dituliskan : X ⊂ Y atau Y ⊃ X.

Operasi-operasi Dasar dalam Diagram Venn:

• Interseksi (Irisan)

C = A ∩B
C = {x ∈ U | (x ∈ A) ∧(x ∈ B)}
Dimana : ∩ menyatakan irisan himpunan| dibaca “sedemikian hingga”∧operator logika AND

• Union (Gabungan) 

C = A ∪ B
C = {x ∈ U | (x ∈ A) ∨(x ∈ B)}
Dimana : ∪ menyatakan gabungan himpunan∨operator logika OR

• Komplemen

A’ = {x ∈ U | ~ (x ∈ A) }
Dimana : ’ menyatakan komplemen himpunan
~ operator logika NOT


Operator Logika
Operator logika yang digunakan :

Kondisional merupakan operator yang analog dengan production rule.
Contoh 1 :
“ Jika hujan turun sekarang maka saya tidak pergi ke pasar”
Kalimat di atas dapat ditulis : p → q
Dimana : p = hujan turun
q = saya tidak pergi ke pasar

Contoh 2 :
p = “Anda berusia 21 atau sudah tua”
q = “Anda mempunyai hak pilih”

Kondisional p → q dapat ditulis/berarti :

Tautologi, Kontradiksi dan Contingent

• Tautologi : pernyataan gabungan yang selalu bernilai benar.
• Kontradiksi : pernyataan gabungan yang selalu bernilai salah.
• Contingent : pernyataan yang bukan tautology ataupun kontradiksi.

Tabel Kebenaran untuk logika konektif :

 Tabel kebenaran untuk negasi konektif :

Resolusi Logika Proposisi
Resolusi merupakan suatu teknik pembuktian yang lebih efisien, sebab fakta-fakta yang akan dioperasikan terlebih dahulu dibawa ke bentuk standar yang sering disebut dengan nama klausa. Pembuktian suatu pernyataan menggunakan resolusi ini dilakukan dengan cara menegasikan pernyataan tersebut, kemudian dicari kontradiksinya dari pernyataan-pernyataan yang sudah ada.
Resolusi adalah suatu aturan untuk melakukan inferensi yang dapat berjalan secara efisien dalam suatu bentuk khusus conjunctive normal form (CNF). Pada logika proposisi, prosedur untuk membuktikan proposisi P dengan beberapa aksioma F yang telah diketahui, dengan menggunakan resolusi.
Algoritma resolusi :
(1) Konversikan semua proposisi F ke bentuk CNF.
(2) Negasikan P, dan konversikan hasil negasi tersebut ke bentuk klausa. Tambahkan ke himpunan klausa yang telah ada pada langkah 1.
(3) Kerjakan hingga terjadi kontradiksi atau proses tidak mengalami kemajuan :
a. Seleksi 2 klausa sebagai klausa parent.
b. Bandingkan (resolve) secara bersama-sama. Klausa hasil resolve tersebut dinamakan resolvent. Jika ada pasangan literal L dan ￢L, eliminir dari resolvent.
c. Jika resolvent berupa klausa kosong, maka ditemukan kontradiksi. Jika tidak, tambahkan ke himpunan klausa yang telah ada.
Contoh :
Diketahui basis pengetahuan (fakta-fakta yang bernilai benar) sebagai berikut:
1. P
2. (P ∧ Q) → R
3. (S ∨ T) → Q
4. T
Buktikanlah kebenaran R!
Pertama-tama kita harus ubah dulu keempat fakta di atas menjadi bentuk CNF. Konversi ke CNF dapat dilakukan sebagai berikut:

Kemudian kita tambahkan kontradiksi pada tujuannya, R menjadi ￢R sehingga fakta-fakta (dalam bentuk CNF) dapat disusun menjadi:
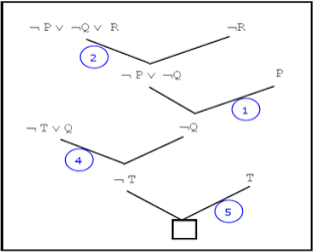
1. P
2. ￢P ∨ ￢Q ∨ R
3. ￢S ∨ Q
4. ￢T ∨ Q
5. T
6. ￢R
Dengan demikian resolusi dapat dilakukan untuk membuktikan R sebagaimana terlihat pada Gambar berikut:

Contoh apabila diterapkan dalam kalimat:
P : Andi anak yang cerdas.
Q : Andi rajin belajar.
R : Andi akan menjadi juara kelas.
S : Andi makannya banyak.
T : Andi istirahatnya cukup.
Kalimat yang terbentuk (basis pengetahuan) menjadi :
1. P : Andi anak yang cerdas.
2. (P ∧ Q) → R : Jika Andi anak yang cerdas dan Andi rajin belajar, maka Andi akan menjadi juara kelas.
3. (S ∨ T) → Q : Jika Andi makannya banyak atau Andi istirahatnya cukup, maka Andi rajin belajar.
4. T : Andi istirahatnya cukup.
Setelah dilakukan konversi ke bentuk CNF, didapat:
1. P : Andi anak yang cerdas.
2. ￢P ∨ ￢Q ∨ R : Andi tidak cerdas atau Andi tidak rajin belajar atau Andi akan menjadi juara kelas.
3. ￢S ∨ Q : Andi tidak makan banyak atau Andi rajin belajar.
4. ￢T ∨ Q : Andi tidak cukup istirahat atau Andi rajin belajar.
5. T : Andi istirahatnya cukup.
6. ￢R : Andi tidak akan menjadi juara kelas.
Pohon aplikasi resolusi untuk kejadian di atas sebagai berikut :

sumber :
 https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=2&ved=0ahUKEwiXmuvjqq3QAhXKvY8KHeS_DkIQFgggMAE&url=http%3A%2F%2Fsupriyan.staff.gunadarma.ac.id%2FDownloads%2Ffiles%2F11876%2F5-Representasi-Pengetahuan-LOGIKA.pdf&usg=AFQjCNGz5Owl96L1dlKqejEc6y8TDVqwow&sig2=gRnlDxO13L9iVOCNTbmG3g&cad=rja
slametgo-blog.blogspot.com/2016/01/resolusi-logika-proposisi.html