METODE PENCARIAN DAN PELACAKAN 2 (HEURISTIK)

Pencarian Heuristik(Heuristic Search)
Heuristik adalah sebuah teknik yang mengembangkan efisiensi dalam proses pencarian, namun dengan kemungkinan mengorbankan kelengkapan (completeness).
Fungsi heuristik digunakan untuk mengevaluasi keadaan - keadaan problema individual dan menentukan seberapa jauh hal tersebut dapat digunakan untuk mendapatkan solusi yang diinginkan.

Best-First Search (Pencarian Terbaik Pertama)
Metode ini merupakan kombinasi dari metode depth-first search dan breadth-first search. Pada metode best-first search, pencarian diperbolehkan mengunjungi node yang ada di level yang lebih rendah, jika ternyata node pada level yang lebih tinggi ternyata memiliki nilai heuristic yang lebih buruk.

Fungsi Heuristik yang digunakan merupakan prakiraan (estimasi) cost dari initial state ke goal state, yang dinyatakan dengan:
                                  f’(n) = g(n) + h’(n)
dimana:

   f’= Fungsi evaluasi
   g = cost dari initial state ke current state
   h’ = prakiraan cost dari current state ke goal state

Misalkan kita memiliki ruang pencarian seperti pada gambar berikut. Node M merupakan keadaan awal dan node T merupakan tujuannya. Biaya edge yang menghubungkan node M dengan node A adalah biaya yang dikeluarkan untuk bergerak dari kota M ke kota A. Nilai g diperoleh berdasarkan biaya edge minimal. Sedangkan nilai h’ di node A merupakan hasil perkiraan terhadap biaya yang diperlukan dari node A untuk sampai ke tujuan. h’(n) bernilai ~ jika sudah jelas tidak ada hubungan antara node n dengan node tujuan(jalan buntu). Kita bisa merunut nilai untuk setiap node.

 

Tabel Status Tiap Node

 

Problem Reduction (Reduksi Masalah) 

Kebanyakan solusi menggunakan pohon OR, dimana lintasan dari awal sampai tujuan tidak terletak pada satu cabang.

Bila lintasan dari keadaan awal sampai tujuan dapat terletak pada satu cabang, maka kita akan dapat menemukan tujuan lebih cepat.

• Graf AND - OR
• Graf AO*

Graf AND - OR
Pada dasarnya samadengan algoritma Best First Search, dengan mempertimbangkan adanya arc AND.
Gambar berikut menunjukkan bahwa untuk mendapatkan TV orang bisa dengan cara singkat yaitu mencuri atau membeli asal mempunyai uang.
Untuk mendeskripsikan algoritma, digunakan nilai F_UTILITY untuk biaya solusi.

Algoritma AND - OR

1. Inisialisasi graf ke node awal.
2. Kerjakan langkah 2 berikut hingganode awal SOLVED atau sampaibiayanya lebih tinggi dari F_UTILITY :

a). Telusuri graf mulai dari node awal dani kuti jalur terbaik. Akumulasikan kumpulan node yang ada pada lintasan tsb. dan belum pernah diekspansi atau diberi label SOLVED.
b). Ambil satu node dan ekspansi node tsb. Jika tidak ada successor maka set F_UTILITY sebagai nilai dari node tsb. Bila tidak demikian, tambahkan successor dari node tsb ke graf dan hitung nilai setiap f’ (hanya gunakan h’ dan abaikan g). Jika f’ = 0 tandai node tsb dengan SOLVED.
c). Ubah f’ harapan dari node baru yang diekspansi. Kirimkan perubahan ini secara backward sepanjanggraf. Jika node berisi suatu arc successor yang semua descendant nya berlabel SOLVED maka tandai node itu dengan SOLVED.

Operasi Reduksi Masalah dengan Graf AND - OR

• Langkah-1 semula hanya ada satu node, A. Node A diekspansi menjadi node B, C dan D. Node D memiliki biaya yang lebih rendah(6) jika dibandingkan dengan B dan C (9).
• Langkah-2 mengekspansi node D menjadi E dan F dengan biaya estimasi sebesar 10. f’ dari D menjadi 10.
• Ternyata level sebelumnya, node B dan C memiliki biaya yang lebih rendah dari D (9 < 10).
• Pada langkah-3 telusuri arc dari A ke B dan C bersama 2. Jika B dieksplore dahulu maka akan menurunkan G dan H. Nilai f’ baru dari B adalah 6 (G = 6 lebih baik dari H = 8) sehingga biaya AND arc B - C menjadi 12 (6 + 4 + 2).
• Dengan demikian nilai node D kembali menjadi lebih baik (10 < 12). Sehingga ekspansi dilakukan kembali terhadap D. dst.

Algoritma AO*
Menggunakan struktur graf. Tiap node pada graf memiliki nilai h’ yang merupakan biaya estimasi jalur dari node itu sendiri sampai suatu solusi.
Algoritma
1. Diketahui graf yang berisi node awal (sebut saja INIT). Hitung h’ (INIT)
2. Kerjakan langkah berikut hingga INIT bertanda SOLVED atau sampai nilai h’ (INIT) > FUTILITY :
    a.) Ekspan INIT dan ambil salah satu node yang belum pernah diekspan (sebutNODE)
    b.) Bangkitkan successor 2 NODE. Jika tidak memiliki successor maka set FUTILITY dengan nilai h’ (NODE). Jika ada successor maka untuk setiap successor (sebut SUCC) yang bukan ancestor dari NODE kerjakan:
         i. Tambahkan SUCC ke graf
         ii. Jika SUCC adalah terminal node tandai dengan SOLVED dan set nilai h’ = 0
         iii.Jika SUCC bukan terminal node, hitung nilai h’.

    c.) Kirimkan informasi baru tsb ke graf dengan cara : tetapkan S adalah node yang ditandai dengan SOLVED atau node yang nilai h’-nya baru saja diperbaiki, dan sampaikan nilai ini ke parent-nya. Inisialisasi S = NODE. Kerjakan langkah berikut ini hingga S kosong:
         i. Jika mungkin, seleksi dari S node yang tidak memiliki descendant dalam gra fyang terjadi pada S. Jika tidak ada, seleksi sembarang node dari S (sebut CURRENT) dan hapus dari S.
         ii. Hitung biaya tiap tiap arc yang muncul dari CURRENT. Biaya ini samadengan jumlah h’ untuk tiap tiap node pada akhir arc ditambah dengan biaya arc itu sendiri. Set h’ (CURRENT) dengan biaya minimum yang baru saja dihitung dari setiap arc yang muncul tadi.
         iii. Tandaijalurterbaikyang keluardariCURRENT denganmenandaiarc yang memilikibiayaminimum.
         iv. Tandai CURRENT dengan SOLVED jika semua node yang dihubungkan dengannya hingga arc yang baru saja ditandai tadi telah ditandai dengan SOLVED.
         v. Jika CURRENT telah ditandai dengan SOLVED atau jika biaya CURRENT telah berubah maka status baru ini harus disampaikan ke graf. Kemudian tambahkan semua ancestor dari CURRENT ke S.

• JalurmelaluiC selalulebihbaikdariB. Tetapijikabiayanode E munculdanpengaruhperubahanyang diberikan ke node B tidak sebesar pengaruhnya terhadap node C maka jalur melalui B bisa lebih baik.
• Hasil ekspan E, misalkan 10, maka biaya node C menjadi 11 (10 + 1), dengan demikian biaya node A apabila melewati C adalah 12 (11 + 1). Tentu saja akan lebih baik memilih melalui node B (11).
• Tapi tidak demikian halnya jika kemudian node D diekspan. Bisa jadi jalur dengan melalui node B akan lebih buruk lagi ketimbang jalur yang melalui node C.

Constraint Satisfaction
Problem search standard :- state adalah "black box“ – setiap struktur data yang mendukung fungsi successor, fungsi heuristik dan tes goal.
CSP:
- state didefinisikan sebagai variabel Xi dengan nilai dari domain Di
- Tes goal adalah sekumpulan constraint yang menspesifikasikan kombinasi dari nilai subset variabel.
Contoh sederhana adalah bahasa representasi formal.
CSP ini merupakan algoritma general-purpose dengan kekuatan lebih daripada algoritma pencarian standar.

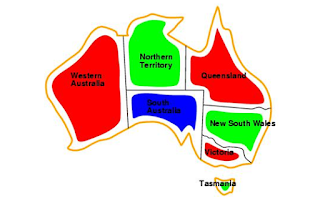
Contoh : Pewarnaan Peta

• Variabel WA, NT, Q, NSW, V, SA, T
• Domain Di = {red,green,blue}
• Constraints : daerah yang bertetangga dekat harus memiliki warna yang berbeda.
• Contoh WA ≠ NT, atau (WA,NT) {(red,green),(red,blue),(green,red), (green,blue),(blue,red),(blue,green)}
• Solusi lengkap dan konsisten, contoh : WA = red, NT = green,Q = red,NSW = green,V = red,SA = blue,T = green

Constraint Graf

• Binary CSP biner : setiap constraint merelasikan dua variabel
• Graf Constraint : node adalah variabel, arc adalah constraint

 

MEA (Means-Ends Analysis)

• MEA adalah strategi penyelesaian masalah yang diperkenalkan pertama kali dalam GPS (General Problem Solver) [Newell & Simon, 1963].
• Proses pencarian berdasarkan ruang masalah yang menggabungkan aspek penalaran forward dan backward.
• Perbedaan antara state current dan goal digunakan untuk mengusulkan operator yang mengurangi perbedaan itu.
• Keterhubungan antara operator dan perbedaan tsb disajikan sebagai pengetahuan dalam sistem (pada GPS dikenal dengan Table of Connections) atau mungkin ditentukan sampai beberapa pemeriksaan operator jika tindakan operator dapat dipenetrasi.
• Contoh OPERATOR first-order predicate calculus dan operator2 tertentu mengijinkan perbedaan korelasi task-independent terhadap operator yang menguranginya.
• Kapan pengetahuan ada tersedia mengenai pentingnya perbedaan, perbedaan yang paling utama terpilih pertama lebih lanjut meningkatkan rata-rata capaian dari MEA di atas strategi pencarian Brute-Force.
• Bagaimanapun, bahkan tanpa pemesanan dari perbedaan menurut arti penting, MEA meningkatkan metode pencarian heuristik lain (di rata-rata kasus) dengan pemusatan pemecahan masalah pada perbedaan yang nyata antara current state dengan goal-nya.

Contoh :

• http://www.rci.rutgers.edu/~cfs/ 472_html/Planning/GPS_472.h tml
• Giarratano – hal 261-262
• Luger – hal 430 - 433.

sumber :
https://aiukswkelasgkelompok7.wordpress.com/metode-pencarian-dan-pelacakan/
slideplayer.info/slide/3764086/
www.slideshare.net/ahmadhaidaroh/modul-3-pencarian-heuristik